Bojan Vukasinovic home page
Individual spray droplets are tracked in successive images and their size, position, trajectory, and instantaneous velocity were determined. Note that each spray droplet acts as a flow marker and hence seeding of the flow was not necessary. A four-frame, forward-backward particle tracking technique is developed and implemented for the velocity measurements in a spray of secondary droplets. The Particle Tracking Velocimetry (PTV) tracks individual droplet images in consecutive image frames and computes the directionally resolved vector for each pair of droplet-images that are matched successfully.
The PTV algorithm developed for this work starts with the detection of individual droplets on the video images. The pre-processed images were thresholded and converted into binary mode with the grayscale light intensity in order to reduce the effects of diffused edges in the droplet images. Droplet images were found and labeled using a line-by-line search of the image file. When a droplet pixel was found, its neighboring pixels were interrogated to see if they were already defined as part of an existing droplet. If yes, the current pixel was labeled as part of that droplet. If no, a new droplet was created and labeled. The cross-sectional area A of each droplet was measured using the sum of the pixels from that droplet. Subsequently, the centroid of each droplet was calculated.
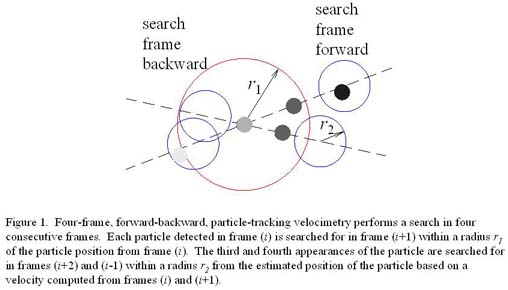
After all centroids were discerned, each droplet in a given image a four-frame, forward-backward search algorithm was used to find a unique matching droplet in the following image. The processing for a given image (i) used the sequence of images: (i-1), (i), (i+1), and (i+2). For each particle in image (i), potential matching particles were found in image (i+1) by searching within a prescribed radius r1 of the original particle’s position. The value of r1 was chosen based on a preliminary knowledge of the approximate maximum velocity of the particles in the flow and the spatial/temporal resolutions of the measurements. For each potential matching particle found in image (i+1), a particle trajectory was determined based on the particle’s locations in images (i) and (i+1) (see Figure 1) and the estimated position of the particle in image (i+2) and (i-1) was determined. These two images were then searched for a particle within a radius r2 of the estimated position. The searching radius r2 was only 2–3 pixels since the particle was expected to be at these locations. If a particle was found in image (i+2) or in image (i-1), or in both, then the particle of image (i+1) was marked as a possible match. If no particles were found in images (i+2) and (i-1), then the potential matching particle of image (i+1) was discarded. After all potential matching particles were examined, only a unique matching particle was accepted. If there were no matches or more than one possible match, then the original particle in image (i) was marked as inconclusive. Once a valid matching particle was found in image (i+1), the velocity vector corresponding to the particle in image (i) was determined. All particle appearances along a valid particle trajectory were then temporally deleted to prevent interference with the remainder of the search process for the particles in a given image.

The application of this algorithm to the VIDA spray is demonstrated in Figure 2. Figure 2a is a superposition of image (i) (light blue) and (i+1) (dark red) showing the detected droplets, their centroids (yellow dots), and the corresponding velocity vectors. Figure 2b is a superposition of all four images used by the particle-tracking algorithm with the centroid of each detected droplet marked by a cross and where the color changes from light to dark as the centroid migrates from images (i-1) to (i+2) (valid velocity vectors are also superimposed on this image). The letters mark three different scenarios encountered by the particle-tracking algorithm. In scenario A, a velocity vector is computed because there is a clear particle path through all four consecutive images. A particle path through three successive images is shown in scenario B, in this case from images (i) to (i+2). A valid velocity vector was still computed for the particle. Finally, in scenario C, a velocity vector was not computed from the particle pair in images (i) and (i+1) because the droplet does not appear in either image (i-1) or (i+2). The most probable reason for this isolated particle pair is out-of-plane motion of the droplet. Note that the particle in image (i+1) is smaller than in image (i), which would be the case when a smaller portion of the droplet is illuminated as it leaves the laser light sheet.

The three characteristic cases are marked by the letters. A letter A denotes case when a vector is accepted because there is a full path of the particle through all four consecutive frames. The vector marked as B is accepted because there is an appearance of the droplet in the three consecutive frames, from n to n+2. Finally, even if it is most likely that the pair of particles marked as C represents the two images of the same droplet, that vector is not accepted because there is no other appearance of the droplet in the frames n-1 and n+2, along the possible path. That criterion is the key in order to prevent the accidental pairing of the traces based on only two consecutive frames, what is the major issue of any two-frame tracking procedure.
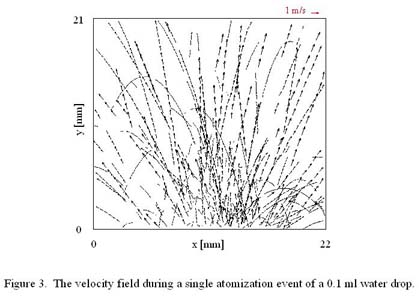
Figure 3 is a composite image showing all of the velocity vectors retrieved from a single bursting event forced at the standard forcing conditions. Initially, most droplet trajectories are roughly normal to the local curvature of the primary drop and are roughly symmetric about the centerline. The initial velocity of the ejected droplets varied substantially from 0.2–2 m/s. This is a direct consequence of the different droplet-ejection mechanisms. It is noteworthy that the present particle-tracking algorithm can determine the velocity of droplets that lose their initial momentum and fall back under gravity. A particle-tracking algorithm that relies on the spatial coherence of particle motion would not be able to track such a particle because it could not distinguish it from adjacent particles moving in the opposite direction.
REFERENCE
back to VIDA